반응형
Notice
Recent Posts
Recent Comments
Link
생활 과학 넘버원
[중학교 3학년 수학] 제곱근과 인수분해가 합쳐진 응용문제 본문
반응형
제곱근과 인수분해가 합쳐지면 재미있는 문제가 됩니다.
이럴 때는 인수분해한 후 그 안에 값을 대입하면 됩니다.
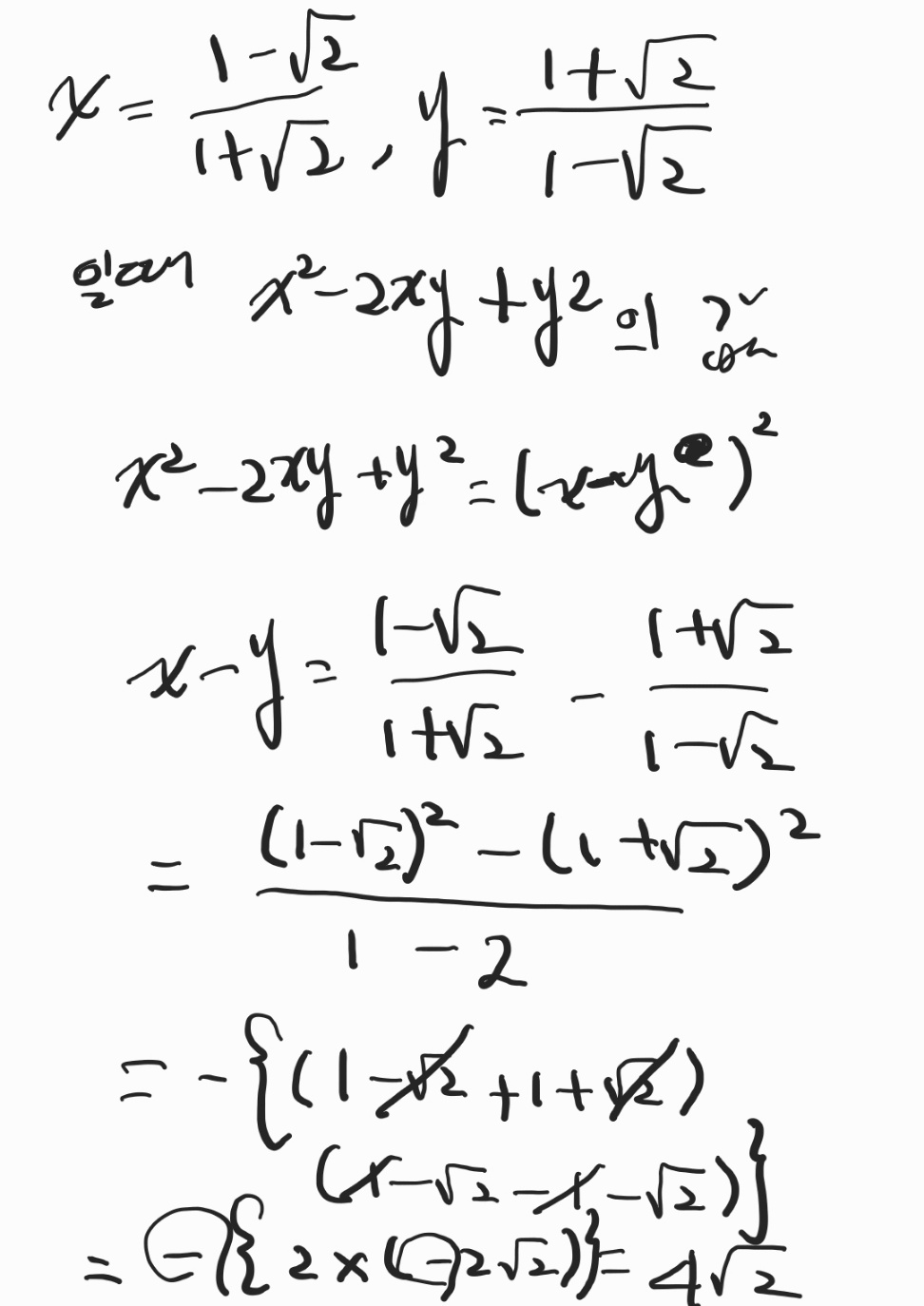
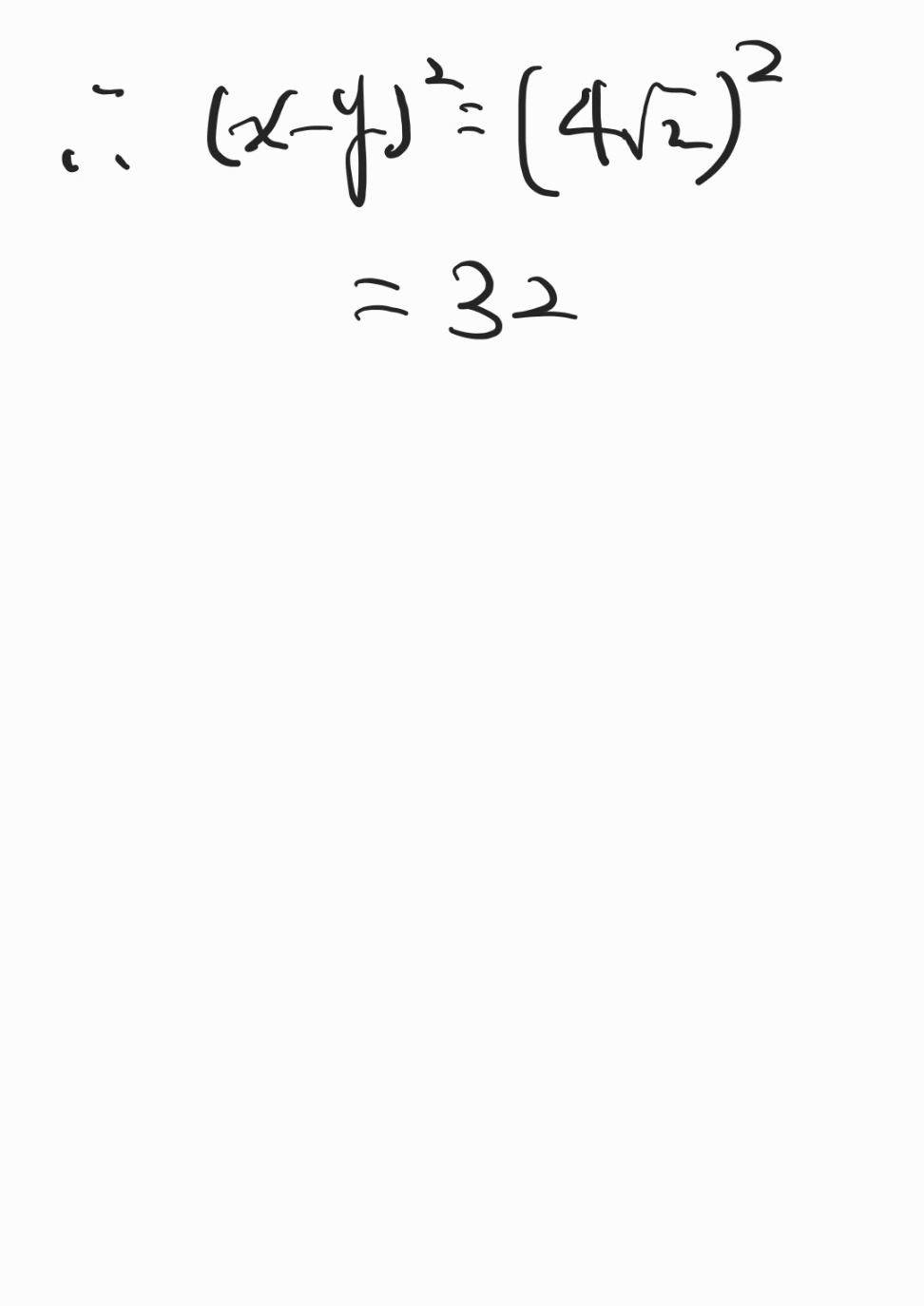
인수분해와 제곱근 값의 연결 문제를 잘 풀기 위해서는 다음과 같은 핵심 개념과 전략을 이해하고 숙련적으로 활용하는 것이 중요합니다.
인수분해와 제곱근 값 연결 문제 풀이 방법
1. 인수분해 기법:
- 공통인수분해: 가장 큰 공통인수를 이용하여 식을 단순화합니다.
- 이차항 인수분해: 이차항을 (a + b)(a - b)와 같은 형태로 분해합니다.
- 삼차항 인수분해: 삼차항을 (a + b)(a^2 - ab + b^2)와 같은 형태로 분해합니다.
- 특수 인수분해: 제곱차, 합차, 평방차 등 특수한 형태의 식을 분해합니다.
2. 제곱근의 개념:
- 완전 제곱수: 제곱근을 구했을 때 정수가 되는 수
- 불완전 제곱수: 제곱근을 구했을 때 정수가 되지 않는 수
- 근사값: 불완전 제곱수의 제곱근을 소수점 아래 몇 자리까지 계산한 값
3. 인수분해와 제곱근 값의 연결:
- 완전 제곱수 인수분해: 완전 제곱수를 (√a)^2와 같은 형태로 분해합니다.
- 불완전 제곱수 인수분해: 불완전 제곱수를 a ± √b와 같은 형태로 분해합니다.
- 제곱근 값 이용: 제곱근 값을 이용하여 식을 단순화합니다.
문제 해결 전략:
- 문제 유형 파악: 문제 유형을 정확하게 파악하여 적절한 해결 전략을 선택합니다.
- 인수분해: 위에서 언급한 인수분해 기법을 활용하여 식을 단순화합니다.
- 제곱근 값 활용: 필요한 경우 제곱근 값을 이용하여 식을 더욱 단순화합니다.
- 답 확인: 답이 정당한지 확인합니다.
연습 및 학습 자료:
- 교과서 및 문제집: 다양한 유형의 문제들을 접하고 해결 방법을 익히는 데 도움이 됩니다.
- 온라인 강의 및 튜토리얼: 인수분해와 제곱근 값에 대한 개념을 이해하고 문제 해결 전략을 배우는 데 도움이 됩니다.
- 문제 풀이 사이트: 다양한 문제들을 풀면서 실력을 향상시킬 수 있습니다.
꾸준한 연습과 노력을 통해 인수분해와 제곱근 값의 연결 문제를 잘 풀 수 있도록 노력하시기 바랍니다.
추가적으로, 다음과 같은 팁을 활용하면 문제 해결에 도움이 될 수 있습니다.
반응형
'중등 고등 중간 기말 고사 대비' 카테고리의 다른 글
| 중학교 수학 1학기 중간고사 보는 방법 (0) | 2024.04.05 |
|---|---|
| [중학교 3학년 수학] 주말에 수학 공부 하는 방법 (1) | 2024.03.30 |
| [중학교 3학년 수학] 3-1 중간고사 수학 대비 인수분해 하는 순서 (1) | 2024.03.26 |
| [중학 수학 3학년] 3-1 중학 수학 중간고사 계산문제 제곱근 관련 (0) | 2024.03.24 |
| [중학 수학 3] 중학교 3-1 중간고사 제곱근 문제 분모의 유리화 (1) | 2024.03.24 |





